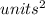Question

Let's see how good you are at math answer this question (if you think your the best)

Answer 1

Explanation:

for the perimeter we just need the distances from point to point

P1(1,1) (x1,y1)

P2(6,2) (x2,y2)

P3(5,4) (x3,y3)

P4(2,5) (x4,y4)

from P1 to P2 is

dist = sqrt [ (x2-x1)^2 +(y2-y1)^2 ]

dist =
`√(26)`

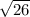
from P2 to P3 is

dist = sqrt [ (x3-x2)^2 +(y3-y2)^2 ]

dist =
`√(5)`

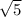
from P3 to P4

dist = sqrt [ (x4-x3)^2 +(y4-y3)^2 ]

dist =
`√(10)`

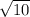
dist = sqrt [ (x1-x4)^2 +(y1-y4)^2 ]

dist =
`√(17)`

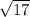
Perimeter is exactly =
`√(26)` +
`√(5)` +
`√(10)` +
`√(17)`

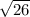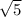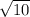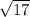
To find the area we have to use the non-right triangle formula of

1/2*a*b*sin(x)

if we knew the angle at P1 then we could find the area of the triangle that is made up by P1, P2 and P4

P1(1,1) (x1,y1)

P2(6,2) (x2,y2)

P3(5,4) (x3,y3)

P4(2,5) (x4,y4)

let's use that fancy slope formula to find the angle

tan(Ф) = abs [ (m1-m2)/(1+m1.m2) ]

m1 = P1P2

m1 = y2-y1 / x2-x1

m1 = 1/5 or .2

m2 = P1P4

m2 = y4-y1 / x4-x1

m2 = 4

now plug into the formula for the angle of P1

tan(Ф) = abs [(0.2 - 5) / (1+0.2*5)]

Ф = arcTan(2.4)

Ф=-67.380135°

the negative signs just means going from P1P4 to P1P2 is -67.380135° we can take it to be positive as well

now plug that angle into our area formula for a non-right triangle

1/2*a*b*sin(x)

area of triangle P1,P2,P4 = 1/2*
`√(26)`*
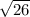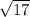`√(17)`*sin(67.380135°)

area P1,P2,P4 = 9.703290477
`units^(2)`

now lets find that other triangle up at the top formed by P2, P3, P4

let's find the slope of the two legs we know the lengths of, of the part that looks a little like a "hat" on top of our 1st triangle

P1(1,1) (x1,y1)

P2(6,2) (x2,y2)

P3(5,4) (x3,y3)

P4(2,5) (x4,y4)

m3= P4P3

m3=y3-y4 / x3-x4

m3 = -1/3

m4 = P3P2

m4 = y2-y3 / x2-x3

m4 = -2/1

m4 = -2

now find the angle between them

tan(Ф) = abs [ (m3-m4)/(1+m3.m4) ]

Ф = arcTan(1)

Ф = 45°

this is the other angle on the 180 line so we have 180-45 =135 as the angle inside our triangle at P3, although, sin 135 and 45 are going to be the same.

now plug that info into our special area of a non-right triangle

area of P2P3P4 = 1/2*
`√(5)`*
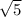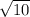`√(10)`*sin(135)

area of P2P3P4 = 2.5

2.5 + 9.703290477 = 12.20329048
`units^(2)`

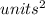
area =12.20329048
`units^(2)`