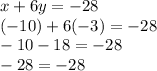Question

Solve the system of equations x+2y=-16 and x+6y=-28 by combining the equations.

Answer 1

x = -10

y = -3

Explanation:

When combining the equations, we must ensure that one of the two variables will cancel out. The easiest way to do this will be to multiply one of the equations by -1, such that the x will cancel out once they are added together. This can be done with either equation, but I will do it for the first one.

This gives us the system:

`\left \{ {{-x-2y=16} \atop {x+6y=-28}} \right.`

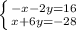
We can then add the two equations by combining each of the terms:

`(x - x) + (6y - 2y) = (-28 + 16)\\(0) + (4y) = (-12)\\4y = -12\\y = -3`

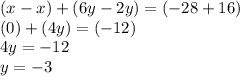
Now that we have the value for y, we substitute it back into any of the original equations and solve for x:

`x + 2y = -16\\x + 2(-3) = -16\\x - 6 = -16\\x = -10`

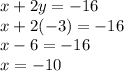
To check our work, we substitute both x and y into the other original equation:

`x + 6y = -28\\(-10) + 6(-3) = -28\\-10 - 18 = -28\\-28 = -28`

Answer 2

x= -18 y=-5/3

Explanation: