Question

Chord AB is 3cm from the center of a circle, the radius of the circle is 5cm, calculate the length of the chord.​

Answer 1

`\large{\boxed{\sf Chord = 8cm }}`

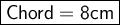
Explanation:

First see figure in attachment . As we know that ,Perpendicular from centre of the circle bisects the chord . Hence here ,

• OC is the perpendicular bisector of chord AB .
• Let us assume that AC = x , therefore ,

`\sf\qquad\longrightarrow AB = 2AC = 2x`

Now in ∆OAC , by Pythagoras Theorem , we have ;

`\sf\qquad\longrightarrow (5cm)^2= x^2+(3cm)^2\\`

`\sf\qquad\longrightarrow 25cm^2=x^2+9cm^2\\`

`\sf\qquad\longrightarrow x^2=25cm^2-9cm^2\\`

`\sf\qquad\longrightarrow x^2=16cm^2\\`

`\sf\qquad\longrightarrow \pink{ x = 4cm }`

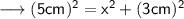
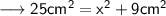
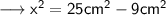
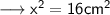
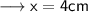
Therefore , the length of chord will be ,

`\sf\qquad\longrightarrow AB = 2x \\`

`\sf\qquad\longrightarrow AB = 2(4cm)\\`

`\sf\qquad\longrightarrow \pink{ AB = 8cm }`

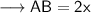
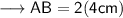
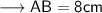
Hence the length of chord is 8cm .