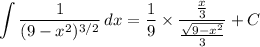Question

Find the indefinite integral using the substitution x = 3 sin(θ). (Use C for the constant of integration.) 1 (9 − x2)3/2 dx

Answer 1

It looks like the integral might be

`\displaystyle \int (9 - x^2)^(3/2) \, dx`

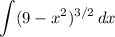
or perhaps

`\displaystyle \int \frac1{(9 - x^2)^(3/2)} \, dx`

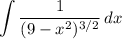
Take note of the fact that both integrands are defined only over the interval -3 < x < 3.

For either integral, we substitute x = 3 sin(θ) and dx = 3 cos(θ) dθ.

Note that we want this substitution to be reversible, so we must restrict -π/2 ≤ θ ≤ π/2, an interval over which sine has an inverse. Then θ = arcsin(x/3).

The first case then reduces to

`\displaystyle \int (9 - (3\sin(\theta))^2)^(3/2) (3 \cos(\theta) \, d\theta) = 3 * 9^(3/2) \int (1 - \sin^2(\theta))^(3/2) \cos(\theta) \, d\theta \\\\ = 81 \int (\cos^2(\theta))^(3/2) \cos(\theta) \, d\theta \\\\ = 81 \int |\cos^3(\theta)| \cos(\theta) \, d\theta`

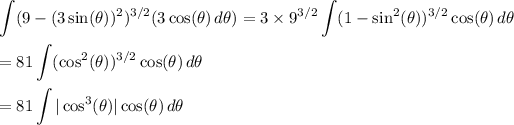
By definition of absolute value,

`\displaystyle 81 \int |\cos^3(\theta)| \cos(\theta) \, d\theta = \begin{cases}\displaystyle 81 \int \cos^4(\theta) \, d\theta & \text{if }\cos(\theta) \ge 0 \\ \displaystyle -81 \int \cos^4(\theta) \, d\theta & \text{if }\cos(\theta) < 0\end{cases}`

and these cases correspond to 0 ≤ θ < π/2 and π/2 < θ ≤ π, respectively. But we are assuming -π/2 ≤ θ ≤ π/2, so the negative case doesn't matter to us.

You can compute the remaining antiderivative by exploiting the half-angle identity for cosine,

`\cos^2(\theta) = \frac{1 + \cos(2\theta)}2`

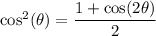
Then

`\cos^4(\theta) = \left(\cos^2(\theta)\right)^2 = \frac{1 + 2\cos(2\theta) + \cos^2(2\theta)}4 = \frac{3 + 4\cos(2\theta) + \cos(4\theta)}8`

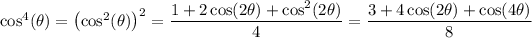
and so

`\displaystyle \int \cos^4(\theta) \, d\theta = (12\theta + 8\sin(2\theta) + \sin(4\theta))/(32) + C`

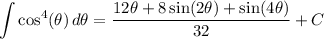
We can simplify this using the double angle identity for (co)sine,

sin(2θ) = 2 sin(θ) cos(θ)

cos(2θ) = 1 - 2 sin²(θ)

as well as the relations,

sin(arcsin(x/3)) = x/3

cos(arcsin(x/3)) = √(9 - x²)/3

which gives us

`\displaystyle \int \cos^4(\theta) \, d\theta = (12\theta + 16 \sin(\theta) \cos(\theta) + 4 \sin(\theta) \cos(\theta) (1 - 2\sin^2(\theta)))/(32) + C`

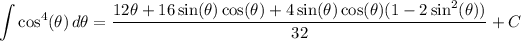
Putting this in terms of x, we get

`\displaystyle \int (9 - x^2)^(3/2) \, dx \\ = 81 * \frac{12\arcsin\left(\frac x3\right) + 16 * \frac x3 * \frac{√(9-x^2)}3 + 4*\frac x3*\frac{√(9-x^2)}3 \left(1 - 2\left(\frac x3\right)^2\right)}{32} + C`

`\displaystyle \int (9 - x^2)^(3/2) \, dx = 81 * \frac{12\arcsin\left(\frac x3\right) + \frac{16x√(9-x^2)}9 + (4x(9-2x^2)√(9-x^2))/(81)}{32} + C`

`\boxed{\displaystyle \int (9 - x^2)^(3/2) \, dx = (12\arcsin\left(\frac x3\right) + (180x-8x^3)√(9-x^2))/(32) + C}`

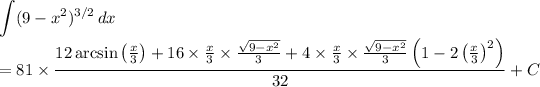
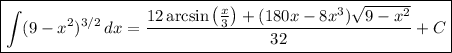
If you were asking about the other integral, the first few steps are similar and you end up with the far more trivial integral and antiderivative

`\displaystyle \frac19 \int (d\theta)/(\cos^2(\theta)) = \frac19 \int \sec^2(\theta) \, d\theta = \frac19 \tan(\theta) + C`

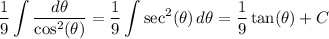
Putting it back in terms of x, we get

`\displaystyle \int \frac1{(9 - x^2)^(3/2)} \, dx = \frac19 \tan\left(\arcsin\left(\frac x3\right)\right) + C`

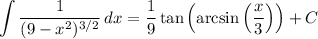
Recall that tan(θ) = sin(θ)/cos(θ), so

`\displaystyle \int \frac1{(9 - x^2)^(3/2)} \, dx = \frac19 * \frac{\frac x3}{\frac{√(9-x^2)}3} + C`

`\boxed{\displaystyle \int \frac1{(9 - x^2)^(3/2)} \, dx = (x)/(9√(9-x^2)) + C}`