Question

Does this limit exist? Show steps

Answer 1

Yes, the limit does exist.

Explanation:

By definition, a limit in the form:

`\displaystyle \lim_(x\to a)f(x)`

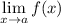
Exists if and only if:

`\displaystyle \lim_(x\to a^-)f(x)=\lim_(x\to a^+)f(x)`

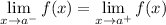
We are given the limit:

`\displaystyle \lim_(x\to 2)(x^2+x-6)/(x^2-4)`

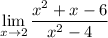
So, in order to prove that this limit exists, we simply have to show that:

`\displaystyle \lim_(x\to 2^-)(x^2+x-6)/(x^2-4)=\displaystyle \lim_(x\to 2^+)(x^2+x-6)/(x^2-4)`

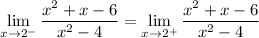
Let's do the left-hand side first. We can factor the function:

`=\displaystyle \lim_(x\to 2^-)((x+3)(x-2))/((x+2)(x-2))`

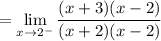
Simplify:

`\displaystyle =\lim_(x\to 2^-)(x+3)/(x+2)`

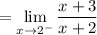
By direct substitution:

`\displaystyle =((2)+3)/((2)+2)=(5)/(4)`

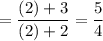
Now, we can evaluate the right-hand side. Again, factor:

`=\displaystyle \lim_(x\to 2^+)((x+3)(x-2))/((x+2)(x-2))`

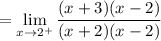
Simplify:

`\displaystyle =\lim_(x\to 2^+)(x+3)/(x+2)`

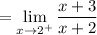
And by direct substitution:

`\displaystyle =((2)+3)/((2)+2)=(5)/(4)`

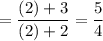
Since both the left- and right-hand limits equal 5/4, our original limit does indeed exist.