Question

James is reading a book and noticed the page numbers are consecutive integers whose product is 1640. What is the value of the larger page number?

Answer 1

41

Explanation:

A pair of consecutive numbers is written as: N and N + 1

(where the larger page number is N + 1)

And we know that the product of these numbers is 1640.

Then:

(N)*(N + 1) = 1640

Solving for N, we get:

N^2 + N = 1640

N^2 + N - 1640 = 0

This is a quadratic equation, remember that for a general quadratic equation:

a*x^2 + b*x + c = 0

The solutions are:

`x = (-b\pm √(b^2 - 4*a*c) )/(2*a)`

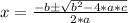
In our case, the solutions are:

`N = (-1 \pm √((1)^2 - 4*1*(-1640)) )/(2) = (1 \pm 81)/(2)`

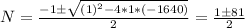
Then the two solutions are:

N = (-1 + 81)/2 = 40

N = (-1 - 81)/2 = -41

Because N represents the number on a page, it only can be a positive value, then we take the positive solution.

Then the two consecutive numbers, N and N + 1

are:

N = 40

N + 1 = 41

The value of the larger page number is 41.