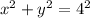Answer:
See below for answers
Explanation:
Given equation of the horizontal ellipse:
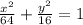
Standard form:
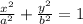
Values of a and b:

Therefore, the radius of the bigger circle is a=r=8 (half the length of the major axis) and the radius of the smaller circle is b=r=4 (half the length of the minor axis).
Given the equation for a circle is
 , then:
, then:
The equation for the larger circle is
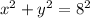
The equation for the smaller circle is