Question

A star with the same mass and diameter as the sun rotates about a central axis with a period of about 24.0 days. Suppose that the sun runs out of nuclear fuel and collapses to form a white dwarf star with a diameter equal to that of the earth. Assume the star acts like a solid sphere and that there is no loss of mass in the process. You will need some data from the inside front cover of you text. (a) What would be the new rotation period (s) of the star? (b) What is the ratio of final to initial kinetic energies (Kf /Ki)?

Answer 1

a) w = 2.52 10⁷ rad / s, b) K / K₀ = 1.19 10⁴

Step-by-step explanation:

a) We can solve this exercise using the conservation of angular momentum.

Initial instant. Before collapse

L₀ = I₀ w₀

Final moment. After the collapse

L_f = I w

angular momentum is conserved

L₀ = L_f

I₀ w₀ = I w (1)

The moment of inertia of a sphere is

I = 2/5 m r²

we take from the table the mass and diameter of the star

m = 1,991 10³⁰ kg

r₀ = 6.96 10⁸ m

r = 6.37 10⁶ m

to find the angular velocity let's use

w = L / T

where the length of a circle is

L = 2π r

T = 24 days (24 h / 1 day) (3600 s / 1h) = 2.0710⁶ s

we substitute

w = 2π r / T

wo = 2π 6.96 10⁸ / 2.07 10⁶

wo = 2.1126 10³ rad / s

we substitute in equation 1

w =
`(I_o)/(I)`

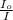
w = 2/5 mr₀² / 2/5 m r² w₀

w = (
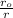`(r_o)/(r)`) ² wo

w = (6.96 10⁸ / 6.37 10⁶) ² 2.1126 10³

w = 2.52 10⁷ rad / s

b) the kinetic energy ratio

K = ½ m w²

K₀ = ½ m w₀²

K = ½ m w²

K / K₀ = (w / wo) ²

K / K₀ = 2.52 10⁷ / 2.1126 10³

K / K₀ = 1.19 10⁴