Question

A particle cannot generally be localized to distances much smaller than its de Broglie wavelength. This means that a slow neutron appears to be larger to a target particle than does a fast neutron, in the sense that the slow neutron will probably be found over a large volume of space. For a thermal neutron at room temperature (300 K), find (a) the linear momentum and (b) the de Broglie wavelength. Compare this effective neutron size with both nuclear and atomic dimensions.

Answer 1

a) p = 1.381 10⁻²⁹ kg m / s, b) λ = 4.80 10⁻⁵ m,

c) λ/a₀ = 9.6 10⁴ = 10⁵, λ/aₙ = 4.80 10⁹

Step-by-step explanation:

a) as the neutral goes at speeds much lower than the speed of light we can use the classical relationships, as the neutral all the thermal energy is the energy of the neutron

E = p c

K T = pc

p = k T / c

p =
`( 1.381 \ 10^(-23) \ 300)/(3 \ 10^8)`

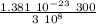
p = 1.381 10⁻²⁹ kg m / s

b) the expression for the de Broglie wavelength

p = h / λ

λ = h / p

λ =
`( 6.63 \ 10^(-34) )/(1.381 \ 10^(-29))`

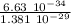
λ = 4.80 10⁻⁵ m

c) let's compare this size with the size of atoms a₀ = 0.5 10⁻⁹ m

λ/a₀ =
`( 4.80 \ 10^(-5) )/(0.5 \ 10^(-9))`

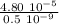
λ/a₀ = 9.6 10⁴ = 10⁵

c) let's compare with the atomic nucleus size aₙ = 10⁻¹⁴ m

λ/aₙ =
`(4.80 \ 10^(-5) )/(10^(-14) )`

λ/aₙ = 4.80 10⁹