Question

Consider the enlargement of the triangle.

A small triangle has a base of 1.7 feet and height of 9.3 feet. A larger triangle has a base of 3.5 feet and height of x feet.
Not drawn to scale

Rounded to the nearest tenth, what is the value of x?
15.8 feet
19.1 feet
23.3 feet
32.6 feet

Answer 1

sorry im late but the answer is B have a good day :)

Explanation:

Answer 2

Given:

After enlargement of the triangle,

Base of small triangle = 1.7 feet

Height of small triangle = 9.3 feet.

Base of larger triangle = 3.5 feet

Height of larger triangle = x feet.

To find:

The value of x.

Solution:

After enlargement the figure is similar to original figure,

We know that the corresponding sides of similar triangles are proportional.

`\frac{\text{Base of small triangle}}{\text{Base of larger triangle}}=\frac{\text{Height of small triangle}}{\text{Height of larger triangle}}`

`(1.7)/(3.5)=(9.3)/(x)`

`1.7* x=9.3* 3.5`

`1.7x=33.55`

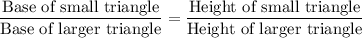
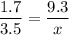
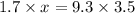
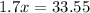
Divide both sides by 1.7.

`x=(32.55)/(1.7)`

`x=19.1470`

`x\approx 19.1`

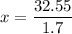
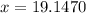
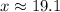
The value of x is 19.1 feet. Therefore, the correct option is B.