Question

Directions: Graph each function using a table of Graph each values, then identify its key characteristics.

1
4. y=(1/2)x
Growth / Decay
»-(
Domain:
Range:
j-intercept:
Asymptote:

Answer 1

Explanation:

Given function is,

`y=((1)/(2))^x`

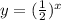
In the given exponential function,

Base of the function =
`(1)/(2)`

By the property of an exponential function,

1). If the base is between 0 and 1, function will be a growth function.

2). If the base is greater than 1, function will be a decay function.

Therefore, given function is a decay function.

Input-output table,

x -2 -1 0 1 2

y
`((1)/(2))^(-2)=4`
`((1)/(2))^(-1)=2`
`((1)/(2))^(0)=1`
`((1)/(2))^1=(1)/(2)`
`((1)/(2))^2=(1)/(4)`

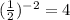
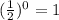
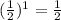
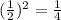
By plotting these points we can get the graph of the function.

Domain: (-∞, ∞)

Range: (0, ∞)

y-intercept: 1

Asymptote: y = 0