Answer:
a) The exponential function is
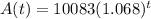
b)
The balance after 1 year is of $10,768.644
The balance after 2 years is of $11,500.91
The balance after 5 years is of $14,010.25.
The balance after 10 years is of $19,467.15
c)
The doubling time is of 10.54 years.
Explanation:
Continuously compounded interest:
The amount of money earning after t years, with interest compounded continuously, is given by:

In which A(0) is the amount of the initial investment and r is the growth rate, as a decimal.
a) Find the exponential function that describes the amount in the account after time t, in years.
Suppose that $10,083 is invested at an interest rate of 6.8% per year
This means, respectively, that
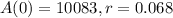
So

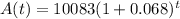
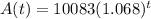
b) What is the balance after 1 year? 2 years? 5 years? 10 years?
After 1 year:
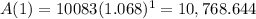
The balance after 1 year is of $10,768.644
After 2 years:
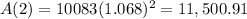
The balance after 2 years is of $11,500.91.
After 5 years:
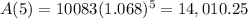
The balance after 5 years is of $14,010.25.
After 10 years:
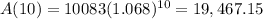
The balance after 10 years is of $19,467.15.
c) What is the doubling time?
This is t for which
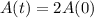 . So
. So
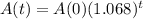
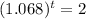

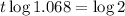
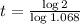
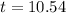
The doubling time is of 10.54 years.