1 Answer

Reconquistador · Answer 1 · 2022-11-30T03:39:20+0000

Given:

In the circle,
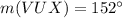$m(\overarc{VUX})=152^\circ$ and
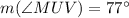$m(\angle MUV)=77^\circ$ .

To find:

The following measures:

(a)
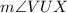
$m\angle VUX$

(b)
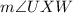
$m\angle UXW$

Solution:

According to the central angle theorem, the central angle is always twice of the subtended angle intercepted on the same same arc.

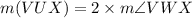
$m(VUX)=2* m\angle VWX$

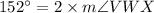
$152^\circ=2* m\angle VWX$

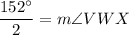
$(152^\circ)/(2)=m\angle VWX$

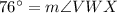
$76^\circ=m\angle VWX$

In a cyclic quadrilateral, the opposite angles are supplementary angles.

UVWX is a cyclic quadrilateral. So,

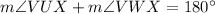$m\angle VUX+m\angle VWX=180^\circ$ [Opposite angles of a cyclic quadrilateral]

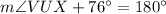
$m\angle VUX+76^\circ=180^\circ$

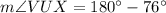
$m\angle VUX=180^\circ-76^\circ$

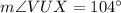
$m\angle VUX=104^\circ$

Now,

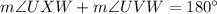$m\angle UXW+m\angle UVW=180^\circ$ [Opposite angles of a cyclic quadrilateral]

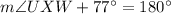
$m\angle UXW+77^\circ =180^\circ$

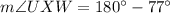
$m\angle UXW=180^\circ-77^\circ$

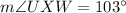
$m\angle UXW=103^\circ$

Therefore,
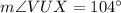$m\angle VUX=104^\circ$ and
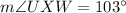$m\angle UXW=103^\circ$ .

Please log in or register to add a comment.