Question

Need help understanding this problem! If someone would explain how to do it that would be great!

In Triangle FGH, FH=6 ft, FG=11 ft, and m *Hint: Law of Cosines

Answer 1

m∠G = 31.83°

Explanation:

From the triangle FGH,

FH = 6 ft

FG = 11 ft

And measure of the included angle ∠F = 73°

We have to find the measure of ∠G.

By applying law of cosine in the triangle to get the measure of third side GH first,

GH² = FH² + FG² - 2(FH)(FG)cos(∠F)

GH² = 6² + 11² - 2(6)(11)cos(73°)

GH² = 36 + 121 - 38.593

GH = √118.407

GH = 10.88 ft

Now apply sine rule in the given triangle to get the measure of ∠G.

`\frac{\text{sinG}}{FH}=\frac{\text{sinF}}{GH}`

`\frac{\text{sinG}}{6}= \frac{\text{sin(73)}}{10.88}`

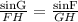
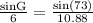
sin(G) = 0.527374

G =
`\text{sin}^(-1)(0.527374)`

m∠G = 31.83°