Answer:
The set of values are described below:
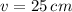 ,
,
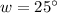 ,
,
 ,
,
 and
and
 .
.
Explanation:
Since
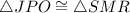 , then
, then
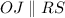 and
and
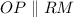 . By Alternate Internal Angles, we find that
. By Alternate Internal Angles, we find that
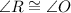 . In addition, the sum of internal angles in triangles equals 180°. Then, we have the following system of linear equations:
. In addition, the sum of internal angles in triangles equals 180°. Then, we have the following system of linear equations:
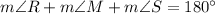 (1)
(1)
 (2)
(2)
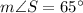 (3)
(3)
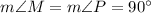 (4)
(4)
The solution of this system is
 ,
,
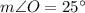 and
and
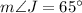 .
.
Lastly, the remaining sides are found by definition of congruence
Segment RS
Since
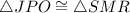 , then
, then
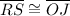 . Hence,
. Hence,
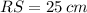
Segment JP
Since
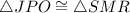 , then
, then
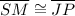 . Hence,
. Hence,
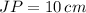
The set of values are described below:
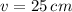 ,
,
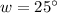 ,
,
 ,
,
 and
and
 .
.