Answer:
The measure of the side
 is 8.8.
is 8.8.
Explanation:
Since
 , then
, then
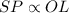 ,
,
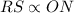 ,
,
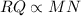 and
and
 . From figure we have the following relationship:
. From figure we have the following relationship:
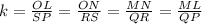 (1)
(1)
Where
 is the proportionality ratio.
is the proportionality ratio.
If we know that
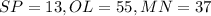 , then the measure of side
, then the measure of side
 is:
is:
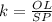 (1b)
(1b)
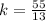
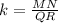
 (1c)
(1c)
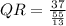
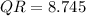
The measure of the side
 is 8.8.
is 8.8.