Answer:
The angle between the two vectors is 84.813°.
Explanation:
Statement is incomplete. Complete form is presented below:
Let be (6,-3, 1) and (8, 9, -11) vector with same origin. Find the angle between the two vectors.
Let
 and
and
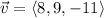 , the angle between the two vectors is determined from definition of dot product:
, the angle between the two vectors is determined from definition of dot product:
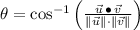 (1)
(1)
Where:
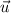 ,
,
 - Vectors.
- Vectors.
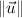 ,
,
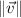 - Norms of each vector.
- Norms of each vector.
Note: The norm of a vector in rectangular form can be determined by either the Pythagorean Theorem or definition of Dot Product.
If we know that
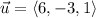 and
and
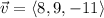 , then the angle between the two vectors is:
, then the angle between the two vectors is:
![\theta = \cos^(-1)\left[\frac{(6)\cdot (8) + (-3)\cdot (9) + (1)\cdot (-11)}{\sqrt{6^(2)+(-3)^(2)+1^(2)}\cdot \sqrt{8^(2)+9^(2)+(-11)^(2)}} \right]](https://img.qammunity.org/2022/formulas/mathematics/high-school/e9dgazib1y3vp9wqf7gf87jex2x9env1j2.png)
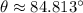
The angle between the two vectors is 84.813°.