Question

One diagonal of the kite is three times as long as the other diagonal. If the area of the kite is 48 square meters, what is the length of each diagonal?​

Answer 1

Given:

One diagonal of the kite is three times as long as the other diagonal.

The area of the kite is 48 square meters.

To find:

The length of each diagonal.

Solution:

We know that, the area of the kite is:

`A=(d_1d_2)/(2)`

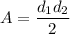
Where,
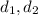`d_1,d_2` are two diagonals of a kite.

It is given that, one diagonal of the kite is three times as long as the other diagonal.

Let
`d_1=3d_2`. Then the area of the kite is:

`A=(3d_2d_2)/(2)`

`A=(3d_2^2)/(2)`

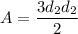
The area of the kite is 48 square meters.

`(3d_2^2)/(2)=48`

`3d_2^2=2(48)`

`d_2^2=(96)/(3)`

`d_2^2=32`

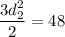
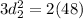
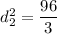
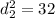
Taking square root on both sides, we get

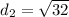`d_2=√(32)` [It is only positive because side length cannot be negative]

`d_2=4√(2)`

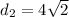
Now,

`d_1=3d_2`

`d_1=3(4√(2))`

`d_1=12√(2)`

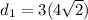
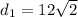
Therefore, the diagonals of the kite are
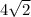`4√(2)` units and
`12√(2)` units.