Question

A running Marites launched the egg she

stole as she was about to be caught with
a velocity of 25 m/s in a direction making
an angle of 20° upward with the
horizontal
a) What is the maximum height reached by
the egg?
b) What is the total flight time (between
launch and touching the ground) of the
egg?
c) What is the horizontal range (maximum
* above ground) of the egg?
d) What is the magnitude of the velocity
of the egg just before it hits the ground?

Answer 1

a) y = 3.73 m, b) t = 1.74 s, c) R = 40.99 m,

d) vₓ = 23.49 m/s, v_y = -8.5 m / s

Step-by-step explanation:

This is a projectile launching exercise, we start by breaking down the initial velocity

sin θ = v_{oy} / v₀

cos θ = v₀ₓ / v₀

v_{oy} = v₀ sin θ

v₀ₓ = v₀ cos θ

v_{oy} = 25 sin 20 = 8.55 m / s

v₀ₓ = 25 cos 20 = 23.49 m / s

a) when the egg reaches the maximum height its vertical speed is zero

v_y² = v_{oy}² - 2 g y

0 = v_[oy}² - 2g y

y = v_{oy}² / 2g

y =
`(8.55^2)/(2 \ 9.8 )`

y = 3.73 m

b) flight time

y = v_{oy} t - ½ g t²

the time of flight occurs when the body reaches the ground y = 0

0 = (v_{oy} - ½ g t) t

The results are

t₁ = 0s this time is for using the body star

v_{oy} - ½ g t = 0

t =
`(2v_(oy)^2)/(g)`

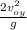
t = 2 8.55 / 9.8

t = 1.74 s

c) the range

R = v₀² sin 2θ / g

R = 25² sin (2 20) / 9.8

R = 40.99 m

d) speed at the point of arrival

horizontal speed is constant

vₓ = v₀ₓ = 23.49 m/s

vertical speed is

v_y = Iv_{oy} - g t

v_y = 8.55 - 9.8 1.74

v_y = -8.5 m / s