Question

The height of a batted baseball is modeled by the equation h(t) = -16t²+64t+6, where t is measured in seconds and h is measured in feet.

a.) At what time in seconds does the ball attain its maximum height?
b.) What is the maximum height attained by the ball? (Give your answer in feet.)

Answer 1

`(dh)/(dt) = - 32t + 64 = 0 \\a) \: t = ( - 64)/( - 32) = 2 \\ \\ b = - 16 * 4 + 64 * 2 + 6 = - 64 + 2 * 64 + 6 = 64 + 6 = 70`

Answer 2

a) t = 2 seconds

b) 70 feet

Explanation:

First of all, we are going to take the derivative of the function (which is a displacement function) to make find its velocity function.

`h(t) = -16t^(2) +64t+6`

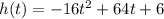
To find the derivative of the equation, we must multiply the coefficient by the exponent and then minus one from the exponent for each term.

`v(t)=(-16)(2)t^(2-1) +64(1)t^(1-1)+6(0)t^(0-1) \\v(t) = -32t +64`

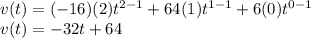
Now we can substitute in v=0

This is because the ball is at the top of its parabola path, it is the turning point and the slope is 0. The velocity physically speaking would also be 0 at the very top of its path.

`0=-32t+64`

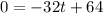
Rearrange and we get:

`32t = 64\\t=2`

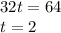
Ball attains maximum height at 2 seconds.

To find the maximum height, we now just have to substitute back in the time into the original equation to find the height.

`h(t) = -16t^(2) +64t+6`

`h(2) = -16(2)^(2) +64(2)+6\\h(2)=-64+128+6\\h(2) = 70`

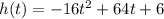
The maximum height attained is 70 feet.

Hope this helped!