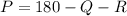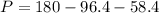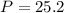Question

Solve triangle PQR. Round intermediate results to 3 decimal places and final answers to 1 decimal place.

Answer 1

`Q = 96.4^\circ`

`R = 58.4`

`P =25.2`

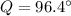
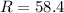
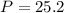
Explanation:

Given

See attachment for PQR

Required

Solve the triangle

From the attached triangle, all sidea of the triangle are known.

i.e.

`PQ = 6\\QR=3\\PR=7`

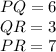
So, we are to solve for
`\angle P, Q \& R`

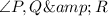
Using cosine rule:

`a^2 = b^2 + c^2 - 2bcCosA`

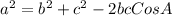
To solve for Q, we have:

`PR^2 = PQ^2 + QR^2 - 2 * PQ * QR Cos(Q)`

`7^2 = 6^2 + 3^2 - 2 * 6 * 3 * \cos(Q)`

`49 = 36 + 9 - 36 * \cos(Q)`

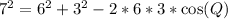
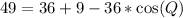
Collect like terms

`49 - 36 - 9 = - 36 * \cos(Q)`

`4 = - 36 * \cos(Q)`

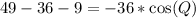
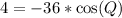
Divide both sides by -36

`\cos(Q) = (-4)/(36)`

`\cos(Q) = -0.1111`

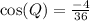
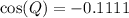
Take arc cos of both sides

`Q = cos^(-1)(0.1111)`

`Q = 96.4^\circ`

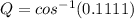
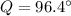
To solve for R, we make use of sine rule;

`(a)/(\sin A) = (b)/(\sin B)`

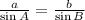
So, we have:

`(PQ)/(\sin R) = (PR)/(\sin Q)`

`(6)/(\sin R) = (7)/(\sin 96.4)`

Cross multiply

`\sin R * 7 = 6 * \sin 96.4`

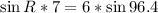
Solve for sin R

`\sin R = (6 * \sin 96.4)/(7)`

`\sin R = (6 * \0.9938)/(7)`

`\sin R = 0.8518`

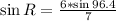
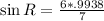
Take arc sin of both sides

`R = sin^(-1)(0.8518)`

`R = 58.4`

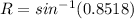
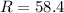
Solving P:

`P+ Q + R = 180` --- angles in a triangle

Solve for P

`P =180-Q-R`

`P =180-96.4-58.4`

`P =25.2`