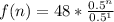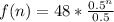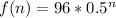Question

F(3) = 12 for a geometric sequence that is defined

recursively by the formula f(n) = 0.5 ∙ f(n – 1), where

n is an integer and n > 0.

Write the equation in explicit form.

Answer 1

`f(n) = 96 * 0.5^n`

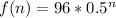
Explanation:

Given

`f(3) = 12`

`f(n) = 0.5 * f(n-1)`

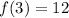
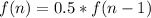
Required

Write as an explicit function

When n = 3, we have:

`f(3) = 12`

`f(3) = 0.5 * f(3-1)`

`f(3) = 0.5 * f(2)`

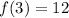
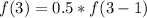
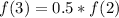
Substitute:
`f(3) = 12`

`12 = 0.5 * f(2)`

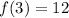
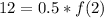
Solve for f(2)

`f(2) = 12/0.5`

`f(2) = 24`

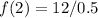
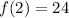
So, we have;

`f(3) = 12`

`f(2) = 24`

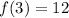
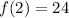
Since it is a geometric sequence, calculate the common ratio (r)

`r = (f(3))/(f(2))`

`r = (12)/(24)`

`r = 0.5`

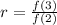
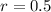
Calculate the first term using:

`r = (f(2))/(f(1))`

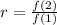
Solve for f(1)

`f(1) = (f(2))/(r)`

`f(1) = (24)/(0.5)`

`f(1) = 48`

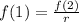
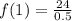
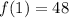
The explicit function is then calculated as:

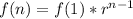`f(n) = f(1) * r^{n-1` ----nth term of a gp

`f(n) = 48 * 0.5^{n-1`

Split the exponent

`f(n) = 48 * (0.5^n)/(0.5^1)`

`f(n) = 48 * (0.5^n)/(0.5)`

`f(n) = 96 * 0.5^n`