Question

An object of mass m is moving in a straight line with velocity v and is slowing down from a force F = -kv where k is a constant. At time t = 0, the velocity is
`v_(0)`. How can I derive an equation for the object's velocity as a function of t?

Answer 1

The equation of the object's velocity in time is
`v(t) = v_(o)\cdot e^{-(k\cdot t)/(m) }`.

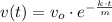Step-by-step explanation:

By Newton's Laws of Motion, the equation of motion that represents the deceleration of the object is described by:

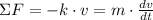`\Sigma F = - k\cdot v = m\cdot (dv)/(dt)` (1)

Where:

`k` - Damping constant, in newton-second per meter.

`m` - Mass, in kilograms.

`v` - Velocity, in meters per second.

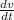`(dv)/(dt)` - Acceleration, in meters per square second.

Then, we modify (1) until the following ordinary differential equation with separable variables is found:

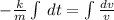`-(k)/(m) \int \, dt = \int {(dv)/(v) }` (2)

Then, we integrate the equation and find the following solution:

`-(k)/(m)\cdot (t-0) = \ln (v)/(v_(o))`

`- (k\cdot t)/(m) = \ln (v)/(v_(o))`

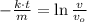
Finally, we clear the velocity in the solution of the differential equation is:

`v(t) = v_(o)\cdot e^{-(k\cdot t)/(m) }`

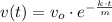
The equation of the object's velocity in time is
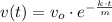`v(t) = v_(o)\cdot e^{-(k\cdot t)/(m) }`.