Answer:
(a) 3003 ways
(b) 10897286400 ways
(c) 3002 ways
Explanation:
Given
 --- 15 players
--- 15 players
Solving (a) Ways of selecting 10 players.
This implies combination.
So, we have:

Using:
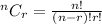
We have:

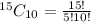
Simplify
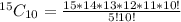
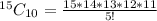
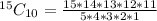
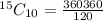
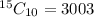
Solving (b) Ways of assigning positions to 10 players.
This implies permutation.
So, we have:

Using:
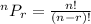
We have:

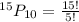
Solve each factorial

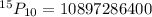
Solving (c) Ways of choosing at least 1 woman
We have:
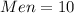
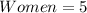
Ways of selecting 10 players is: (a) 3003 ways
Since the number of men are 10, there is 1 way of selecting 10 men (i.e. selection without women)
Using complement rule:
At least 1 woman = Total - No woman

