Question

You and a friend are playing with a bowling ball to demonstrate some ideas of Rotational Physics. First, though, you want to calculate the Rotational Kinetic Energy of the bowling ball as it rolls down a sidewalk without slipping. This means it has both linear kinetic energy and rotational kinetic energy. A bowling ball can be modeled as a solid sphere rotating about its center. This bowling ball has a mass of 6.40 kg and a radius of 0.130 m. You'll need to look up the equation for the Moment of Inertia in your textbook. It is rotating with an angular velocity of 16.0 radians / second in the counter-clockwise (or positive) direction. You can use this to determine the linear velocity of the bowling ball (since it is rolling without slipping). What is the Total Kinetic Energy of the bowling ball

Answer 1

K_{total} = 19.4 J

Step-by-step explanation:

The total kinetic energy that is formed by the linear part and the rotational part is requested

`K_(total) = K_(traslation) + K_(rotation)`

let's look for each energy

linear

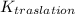`K_(traslation)` = ½ m v²

rotation

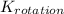`K_(rotation)` = ½ I w²

the moment of inertia of a solid sphere is

I = 2/5 m r²

we substitute

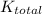`K_(total)` = ½ mv² + ½ I w²

angular and linear velocity are related

v = w r

we substitute

K_{total} = ½ m w² r² + ½ (2/5 m r²) w²

K_{total} = m w² r² (½ + 1/5)

K_{total} =
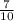`(7)/(10)` m w² r²

let's calculate

K_{total} =
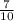`(7)/(10)` 6.40 16.0² 0.130²

K_{total} = 19.4 J