Question

A circular carnival ride has a diameter of 120 ft. Suppose you board a gondola at

the bottom of the circular ride, which is 6 ft above the ground, and rotate 240°

counterclockwise before the ride temporarily stops. How many feet above ground

are you when the ride stops?

Answer 1

The height above ground when the ride stops is 96 feet

Explanation:

The given diameter of the carnival ride, d = 120 ft.

The height of the ride above the ground, h = 6 ft.

The angle through which the ride is rotated, θ = 240° counterclockwise

Therefore, we have;

The radius of the ride, r = d/2

∴ r = 120 ft./2 = 60 ft.

We note that at 180° rotation, the ride is at the highest point,
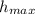`h_(max)` = 6 ft. + 120 ft. = 126 ft.

When the ride rotates a further 240° - 180° = 60° the height drops from the maximum point by y = 60 ft. × cos (60°) = 30 ft., such that the final height above ground is therefore;

h = 126 ft. - 30 ft. = 96 ft.

The height above ground when the ride stops, h = 96 ft.