Question

A) The mean is _____. *

b) The standard deviation is _____. *



c) Approximately _____ % of the data values fall between 223 and 237. *


This is a required question
d) Approximately _____ % of the data values fall between 216 and 244.

e) Approximately _____ % of the data values fall between 209 and 251.

Answer 1

If all of the observed values in a sample are close to the sample mean, the standard deviation will be small (i.e., close to zero), and if the observed values vary widely around the sample mean, the standard deviation will be large. If all of the values in the sample are identical, the sample standard deviation will be zero.

Explanation:

Answer 2

a) The mean is 230.

b) The standard deviation is approximately 15.11.

c) Approximately 35.11% of the data values fall between 223 and 237.

d) Approximately 67.45% of the data values fall between 216 and 244.

e) Approximately 80.23% of the data values fall between 209 and 251.

How to find the mean of the given data points

a) To find the mean of the given data points, sum them up and divide by the number of data points (which is 7 in this case).

Mean = (209 + 216 + 223 + 230 + 237 + 244 + 251) / 7 = 1610 / 7 = 230.

Therefore, the mean is 230.

b) To find the standard deviation of the given data points, use the formula for sample standard deviation:

Standard Deviation =
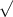`\sqrt`((sum of (data points - mean)^2) / (n - 1))

where n is the number of data points.

Standard Deviation =
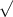`\sqrt`((sum of
`[(209 - 230)^2 + (216 - 230)^2 + (223 - 230)^2 + (230 - 230)^2 + (237 - 230)^2 + (244 - 230)^2 + (251 - 230)^2]) / 6)`

Standard Deviation =
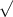`\sqrt`((sum of [441 + 196 + 49 + 0 + 49 + 196 + 441]) / 6)

Standard Deviation =
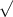`\sqrt`(1372 / 6) ≈
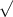`\sqrt`(228.67) ≈ 15.11 (rounded to two decimal places).

Therefore, the standard deviation is approximately 15.11.

c) To find the percentage of data values that fall between 223 and 237, calculate the z-scores for these values and then use a standard normal distribution table to find the corresponding probabilities.

The z-score for 223 is (223 - mean) / standard deviation = (223 - 230) / 15.11 ≈ -0.46.

The z-score for 237 is (237 - mean) / standard deviation = (237 - 230) / 15.11 ≈ 0.46.

Using the standard normal distribution table, the area between -0.46 and 0.46 is approximately 0.3511.

Therefore, approximately 35.11% of the data values fall between 223 and 237.

d) To find the percentage of data values that fall between 216 and 244, repeat the same process as in part (c).

The z-score for 216 is (216 - mean) / standard deviation = (216 - 230) / 15.11 ≈ -0.93.

The z-score for 244 is (244 - mean) / standard deviation = (244 - 230) / 15.11 ≈ 0.93.

Using the standard normal distribution table, the area between -0.93 and 0.93 is approximately 0.6745.

Therefore, approximately 67.45% of the data values fall between 216 and 244.

e) To find the percentage of data values that fall between 209 and 251, repeat the same process as in part (c).

The z-score for 209 is (209 - mean) / standard deviation = (209 - 230) / 15.11 ≈ -1.39.

The z-score for 251 is (251 - mean) / standard deviation = (251 - 230) / 15.11 ≈ 1.39.

Using the standard normal distribution table, the area between -1.39 and 1.39 is approximately 0.8023.

Therefore, approximately 80.23% of the data values fall between 209 and 251.