Answer:
![g(x)=-2\sqrt[3]x](https://img.qammunity.org/2022/formulas/mathematics/high-school/hr6b662uhk0c2hcrzkf1b40985wcdf3bp1.png)
or

Explanation:
Given
![f(x) = \sqrt[3]x](https://img.qammunity.org/2022/formulas/mathematics/high-school/fkoetg7pbyiwedm51pztkijx2izrjctsc9.png)
Required
Write a rule for g(x)
See attachment for grid
From the attachment, we have:
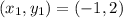
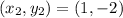
We can represent g(x) as:
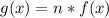
So, we have:
![g(x) = n * \sqrt[3]x](https://img.qammunity.org/2022/formulas/mathematics/high-school/hsbc88653m2f5ekibmw6yj6veb2nswqppc.png)
For:
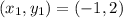
![2 = n * \sqrt[3]{-1}](https://img.qammunity.org/2022/formulas/mathematics/high-school/50ny35ccgq7r7ox803llslqda3a6vh8vn8.png)
This gives:
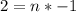
Solve for n
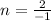

To confirm this value of n, we make use of:
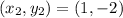
So, we have:
![-2 = n * \sqrt[3]1](https://img.qammunity.org/2022/formulas/mathematics/high-school/qz619f19p59bq6kbbaompg8ikl19dnys02.png)
This gives:

Solve for n
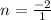

Hence:
![g(x) = n * \sqrt[3]x](https://img.qammunity.org/2022/formulas/mathematics/high-school/hsbc88653m2f5ekibmw6yj6veb2nswqppc.png)
![g(x)=-2\sqrt[3]x](https://img.qammunity.org/2022/formulas/mathematics/high-school/hr6b662uhk0c2hcrzkf1b40985wcdf3bp1.png)
or:
