Question

There is a bottleneck in producing masses higher than4He, because there are no mass-5or mass-8 stable nuclides. For older stars with high densities and high temperatures (T>100 million K), three alpha particles can form12C. This occurs by two alpha particles firstforming8Be, and then8Be reacting with another alpha particle to form12C before8Be candecay back to two alpha particles.a) Explain why this can only happen in very hot stars and high density.b) Calculate how much energy is given up when three alpha particles form12C.

Answer 1

Step-by-step explanation:

a)

To pass the Coulomb barriers and undergo nuclear fusion, alpha particles must be burned at high temperatures. As a result, the ignition temperature needed for this reaction is 5.4168 × 10¹⁰ K. Helium must be burned at a high temperature and density. As a result, this must occur for hot stars with high densities.

b)

The amount of energy given up can be calculated as follows:

`_2He^4 + _2He^4 \to _4Be^8 ---- (1) \\ \\ _4Be^8 + 2_He^4 \to _6C^(12) ---(2)`

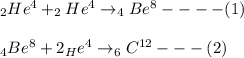
where;

`M(_2He^4) = 4.002603 \ u \\ \\ M(_4Be^8) = 8.005305 10 \ u`

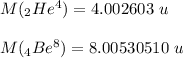
Therefore, from the reaction (1);

`Q = \Big ( M(_2He^4) + M(_2He^4) - M(_4Be^8) \Big ) ( 931.5 \ MeV) \\ \\ = \Big ( 2(4.002603 \ u) - (8.00530510 \ u) \Big) \Big ( 931.5 \ MeV/u \Big) \ \\ \mathbf{= -0.092 \ MeV}`

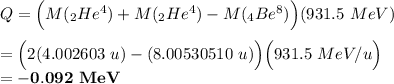
From the second reaction:

`Q = \Big ( M(_4Be^8) + M(_2He^4) - M(_6C^(12)) \Big ) ( 931.5 \ MeV) \\ \\ = \Big ( 8.00530510 \ u +4.002603 \ u -12 \ u \Big) \Big ( 931.5 \ MeV/u \Big) \ \\ \mathbf{= 7.37 \ MeV}`