Question

Find the length of the hypotenuse of an isosceles right triangle of area 72cm square​

Answer 1

`\large{\boxed{\sf Hypotenuse = 16.97\ cm }}`

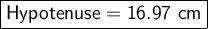
Explanation:

Here it is given that the area of a right isosceles ∆ is 72 cm² . Let us assume that each equal side is x . Therefore the height and the base of the ∆ will be same that is x .

`\sf\qquad\longrightarrow Area =(1)/(2)(base)(height)\\`

`\sf\qquad\longrightarrow 72cm^2=(1)/(2)(x)(x)\\`

`\sf\qquad\longrightarrow x^2= 144cm^2\\`

`\sf\qquad\longrightarrow x =√(144cm^2)\\`

`\sf\qquad\longrightarrow \pink{x = 12cm }`

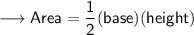
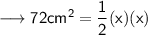
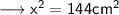
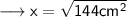
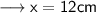
Hence we may find hypotenuse using Pythagoras Theorem as ,

`\sf\qquad\longrightarrow h =√( p^2+b^2)`

• Here p = b = 12cm ,

`\sf\qquad\longrightarrow h =√( (12cm)^2+(12cm)^2)\\`

`\sf\qquad\longrightarrow h =√(144cm^2+144cm^2)\\`

`\sf\qquad\longrightarrow h =√(288cm^2)\\`

`\sf\qquad\longrightarrow \pink{ hypotenuse= 16.97cm }`

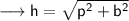
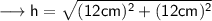
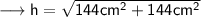
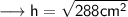
Hence the hypotenuse is 16.97 cm .

Answer 2

Explanation:

The base and height will be the two equal sides of the isosceles right triangle.

⇒ b = h = x cm

`Area \ of \ triangle = (1)/(2)bh`

`(1)/(2)bh = 72 \ cm^(2)`

`(1)/(2)*x*x=72\\\\\\(1)/(2)*x^(2)=72\\\\\\x^(2)=72*2\\\\x^(2)=144\\\\Take \ square \ root,\\\\\sqrt{x^(2)}=√(144)\\\\x = √(12*12)\\\\x = 12 cm`

Hypotenuse² = b² + h²

= 12² + 12²

= 144 + 144

= 288

hypotenuse = √288

= 16.97 cm