Answer:
The functions have the same y-intercept.
OPTION C is correct.
Explanation:
DEFINITIONS AND FORMULAS
The equation of a linear graph is given to be:

Where m is the slope of the graph and b is the y-intercept.
To calculate the slope given a table, we can use the formula:
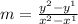
SOLUTION
Function 1: The equation of the graph is given to be
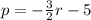
Therefore, the y-intercept of the graph is given to be:
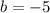
Function 2: Recall that the y-intercept of a graph is the y-value when x = 0.
On checking the graph, we can see that when r = 0, p = -5.
Therefore, the y-intercept is:
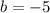
ANSWER
The functions have the same y-intercept.
OPTION C is correct.