Question

A whole set of birdfeeders are designed using conservation of Angular Momentum to spin when a squirrel jumps on them. This can throw the squirrel off (though not all squirrels give up that easily - see this video for an example). A bird, landing, doesn't cause the same problem. A squirrel, with a mass of 3.00 kg launches itself at the bird feeder with a velocity of 3.40 m/s. The bird feeder has a radius of 6.30 cm and a Moment of Inertia of 2.00 kg m2. Initially the bird feeder is not rotating at all, but starts rotating when the squirrel lands on the outer edge (at the same radius as described above). You can assume that the squirrel is small compared to the size of the bird feeder radius (not true in the video, but it does make this a bit easier for out calculations). What is the angular velocity of the bird feeder - squirrel system after the squirrel lands on it

Answer 1

w = 0.319 rad / s

Step-by-step explanation:

This is an angular momentum problem, let's form a system composed of the feeder and the squirrel, therefore the forces during the collision are internal and the angular momentum is conserved.

initial instant. Before the squirrel jumps

L₀ = m v r

final instant. After the trough and the squirrel are together

L_f = (I_fetter + I_ardilla) w

angular momentum is conserved

L₀ = L_f

m v r = (I_fetter + I_ardilla) w

w =
`(mvr)/(I_(fetter) + I_(ardilla) )`

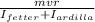
the moment inercial ofbody is

I_thed = 2.00 kg m²

We approach the squirrel to a specific mass

I_ardilla = m r²

we substitute

w = m v r / ( I_[feefer + m r²)

let's calculate

w = 3 3.40 6.30 10⁻² / (2.00 + 3.00 (6.30 10-2)² )

w = 0.6426 / 2.0119

w = 0.319 rad / s