Answer:
Step-by-step explanation:
From the given information:
Strain fracture toughness
 = 75 MPa
= 75 MPa
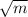
Tensile stress
 = 361 MPa
= 361 MPa
Value of Y = 1.03
Thus, the minimum length of the critical interior surface crack which will result to fracture can be determined by using the formula:
![a_c = (1)/(\pi) ( (k_k)/(\sigma Y))^2 \\ \\ a_c = (1)/(\pi) \Big [ (75 * √(10^3))/(361 * 1.03 ) \Big]^2 \\ \\ a_c = (1)/(\pi) \Big [ 6.378474693\Big]^2 \\ \\ \mathbf{ a_c = 12.95 \ mm}](https://img.qammunity.org/2022/formulas/engineering/college/jrhukc8yz8fjens8nzvtocz9myiiv4jxge.png)