Answer:
the average speed of the particles in terms of the speed of light is 0.81c
Step-by-step explanation:
Given the data in the question;
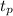 = 256.2 ps = 256.2 × 10⁻¹² s
= 256.2 ps = 256.2 × 10⁻¹² s
speed of light c = 2.99 × 10⁸ m/s
d = 10.7 cm = 0.107 m
we know that; Average speed v = d/t ------- let this be equation 1
Also, given that 256.2 ps is the lifetime of particle X frame, proper time will be;
t = Y
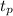 =
=
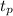 / √( 1 -
/ √( 1 -
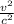 ) --------- let this be equation 2
) --------- let this be equation 2
Next, we input equation 2 into equation 1'
v = d / [
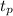 / √( 1 -
/ √( 1 -
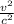 ) ]
) ]
v = d/
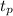 [ √( 1 -
[ √( 1 -
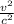 ) ]
) ]
v
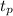 /d = √( 1 -
/d = √( 1 -
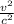 )
)
we square both sides
( v
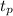 /d )² = (√( 1 -
/d )² = (√( 1 -
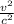 ) )²
) )²
v²
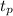 ²/d² = 1 -
²/d² = 1 -
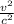
v²
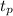 ²/d² +
²/d² +
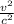 = 1
= 1
v²(
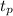 ²/d² +
²/d² +
 ) = 1
) = 1
v²( (
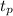 ²c² + d²)/d²c² ) = 1
²c² + d²)/d²c² ) = 1
∴
v² = (d²c²) / (
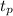 ²c² + d²)
²c² + d²)
v = √[ (d²c²) / (
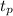 ²c² + d²) ]
²c² + d²) ]
v = (dc) / √(
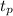 ²c² + d²)
²c² + d²)
so we substitute
v = (0.107 m × c) / √( (256.2 × 10⁻¹² s)²(2.99 × 10⁸ m/s)² + (0.107 m )²)
v = 0.107c / √( 0.00586814 + 0.011449 )
v = 0.107c / √( 0.01731714 )
v = 0.107c / 0.1315946
v = 0.81c
Therefore, the average speed of the particles in terms of the speed of light is 0.81c