Question

Please help me! Please! I am so lost! Pythagorean Theorem!

(The prism said to have an equilateral triangle base has the measurements shown)

Part A
Are the bases of the prism equilateral triangle‘s? Why or why not? Note: the bases of a triangular prism are triangles.

Part B
For this prism to be a right prism, all the lateral faces must be rectangles. Is enough information given to prove the lateral faces are rectangles? Why or why not?

Part C
Without using a protractor, you can determine whether the angles are right angles by measuring the length of the diagonal and applying the converse of the Pythagorean theorem.
The length of both diagonals for each lateral side is 13 cm. From this can you prove that the lateral sides are rectangles? Why or why not?

Part D
Some of the measurements of the triangular prism with a right angle base are shown. What is the length of the hypotenuse of the base?

Part E
Which lateral face has the largest area, the bottom one, left one, or diagonal one? What is the area?

Answer 1

Part A- yes, because all 3 sides are Equal (each side is 5)

Part B- yes, each rectangle has the dimensions 12*5

Part C- yes- since the sides are 5 and 12 you can determine that the diagonal is 13, using they Pythagorean theorem
`a^(2) +b^(2) =c^(2)`

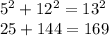`5^(2) +12^(2) =13^(2) \\25+144=169`- true statement, so the lateral sides are rectangles, because the corners are 90

Part D-
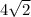`4√(2)` (it is a 45-45-90 triangle- so the hypotenuse is the side length times
`√(2)`

Part E- the diagonal face as the largest area- dimensions are
`4√(2) * 12\\`

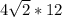
the area would be
`48√(2)`

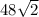
Explanation: