Answer: 2
========================================================
Step-by-step explanation:
Recall that any exponential equation of the form
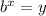 can be written into its equivalent log form of
can be written into its equivalent log form of
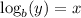 . Note how in both cases, 'b' is the base. For the exponential equation, x is buried in the exponent and y is free on its own. In the log equation, we have y buried in the log and x is free or isolated on its own.
. Note how in both cases, 'b' is the base. For the exponential equation, x is buried in the exponent and y is free on its own. In the log equation, we have y buried in the log and x is free or isolated on its own.
In your case, we have b = 7 and y = 49. This means
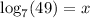 is the same as
is the same as
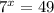 when converting from log form to exponential form. Then we can rewrite that 49 into 7^2 to get
when converting from log form to exponential form. Then we can rewrite that 49 into 7^2 to get
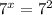 . The bases are both 7, so the exponents must be the same as well. Therefore, x = 2.
. The bases are both 7, so the exponents must be the same as well. Therefore, x = 2.
-------------------
We could follow a different approach. We could apply the change of base formula. The change of base formula is
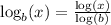
On the left side, we have log base b; however, on the right side, the log can be any base we want. Oftentimes it's handy to go with base 10, though again it doesn't matter the base on the right hand side logs.
So we would then say...

Due to rounding error, we don't land exactly on 2 as expected. However, we get close enough.