Question

A penny is dropped from a height of 144 ft. Calculate the time between when the rock was dropped and when it landed. If we choose "down" as positive and ignore air friction, the function is h(t) = 16t^2 - 144.

answers
t = 9seconds
t = 3 seconds
t = 18 seconds
t = 10 seconds ​

Answer 1

t= 3 seconds

Explanation:

I took the quiz and this is the answer

Answer 2

The time of fall is 9 seconds

Explanation:

We are asked to find the time between when the penny was dropped and when it landed.

To do this, we have to start with what we are given and see how we can relate it to find what we are looking for.

From the problem, we are given the equation which represents the height which the penny travels as it falls. It is given by

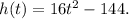`h(t) = 16t^2 - 144.` ----------- equation 1

in addition to that, we are also given that h = 144ft at the end of the fall; that is, where t = t max, and h = hmax

Hence, it is safe to say that at the end of the fall, that the heigh is no more changing. This means that dh/dt = 0

We can now differentiate equation 1 above to get

h max = 16t - 0 ------------- equation 2

recall that h max = 144

plugging the value of h max into equation 2, we have

144 = 16t

t = 9 seconds

Therefore the time of fall is 9 seconds