Answer:
The square roots of 49·i in ascending order are;
1) -7·(cos(45°) + i·sin(45°))
2) 7·(cos(45°) + i·sin(45°))
Explanation:
The square root of complex numbers 49·i is found as follows;
x + y·i = r·(cosθ + i·sinθ)
Where;
r = √(x² + y²)
θ = arctan(y/x)
Therefore;
49·i = 0 + 49·i
Therefore, we have;
r = √(0² + 49²) = 49
θ = arctan(49/0) → 90°
Therefore, we have;
49·i = 49·(cos(90°) + i·sin(90°)
By De Moivre's formula, we have;
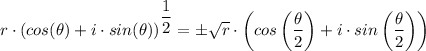
Therefore;
√(49·i) = √(49·(cos(90°) + i·sin(90°)) = ± √49·(cos(90°/2) + i·sin(90°/2))
∴ √(49·i) = ± √49·(cos(90°/2) + i·sin(90°/2)) = ± 7·(cos(45°) + i·sin(45°))
√(49·i) = ± 7·(cos(45°) + i·sin(45°))
The square roots of 49·i in ascending order are;
√(49·i) = - 7·(cos(45°) + i·sin(45°)) and 7·(cos(45°) + i·sin(45°))