Answer:
D.
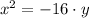
Explanation:
The vertex form of the equation of the parabola centered in the origin, with axis of symmetry in the x-axis and directrix in the first and second quadrants is described by the following formula:
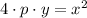 ,
,
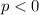 (1)
(1)
Where:
 - Dependent variable.
- Dependent variable.
 - Independent variable.
- Independent variable.
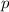 - Focus distance.
- Focus distance.
If we know that vertex is located at (0, 0) and the directrix pass through (4, 0), then the focus distance (distance of the vertex with respect to that point) is -4, and the equation of the parabola is
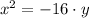 .
.
Hence, the right choice is D.