Question

How am I supposed to do this?

Answer 1

The two-sided limit exists as long as the limits from either side also exist and are equal. So to compute the limit, you have to compute the one-sided limits,

`\displaystyle\lim_(x\to0^-)f(x)`

`\displaystyle\lim_(x\to0^+)f(x)`

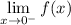
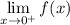
f(x) has a different definition and thus different behavior as x approaches 0 depending on which direction x is approaching 0:

• When x approaches 0 from the left (or from below), you use the definition of f for x < 0, so

`\displaystyle\lim_(x\to0^-)f(x) = \lim_(x\to0)(-x-2) = -2`

• When x approaches 0 from the right (or above), you use the other definition, so

`\displaystyle\lim_(x\to0^+)f(x) = \lim_(x\to0) \left(\frac x2-2\right) = -2`

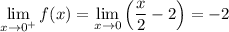
The limits from either side match, so the two-sided limit exists and is also -2.