Here, We have given
- The sides of a triangle are 8 , 15 and 18
- The one of the side of the similar traingle is 10.
Let assume the given triangle as ΔABC and ΔXYZ
According to the similarity theorem
- If two triangle's are similar then the ratio of their corresponding sides are also equal .
Therefore, By using above theorem :-
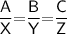
Subsitute the required values
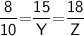
For other two sides of another similar triangle
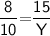
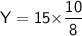
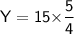
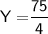
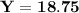
And,
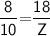

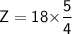
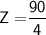
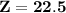
Hence, The two sides of the another similar triangle is 18.75 and 22.5

Here, We have
- Two similar triangles
- Whose sides are 4 , 12 ,20 and 5 , 15 , 25
Let assume the two triangle be ΔABC and ΔPQR
According to the similarity theorem :-
- If two triangle's are similar then the ratio of their corresponding sides are also equal .
That is,
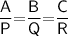
Subsitute the required values,
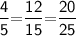

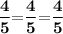
Hence, The scale factor of the given similar triangles is 4/5
Here, we have given that
- A map in Davao City has a scale factor of 1 cm to 0.5 km
- That is,
- 1 : 0.5
But,
- We have to find the distance corresponds to an actual distance of 12 km.
Therefore,
According to the scale factor
The actual distance will be
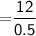
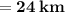
Hence, The map distance corresponds to actual distance of 12 km is 24 km.