Question

Find the derivative of 1/x^4/3

Answer 1

`\displaystyle (dy)/(dx) = (-4)/(3x^5)`

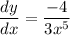
General Formulas and Concepts:

Calculus

Differentiation

• Derivatives
• Derivative Notation

Derivative Property [Multiplied Constant]:
`\displaystyle (d)/(dx) [cf(x)] = c \cdot f'(x)`

Basic Power Rule:

1. f(x) = cxⁿ
2. f’(x) = c·nxⁿ⁻¹

Explanation:

Step 1: Define

Identify

`\displaystyle y = ((1)/(x^4))/(3)`

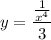
Step 2: Differentiate

1. Derivative Property [Addition/Subtraction]:
   `\displaystyle y' = (1)/(3) (d)/(dx) \bigg[ (1)/(x^4) \bigg]`
2. Rewrite:
   `\displaystyle y' = (1)/(3) (d)/(dx)[x^(-4)]`
3. Basic Power Rule:
   `\displaystyle y' = (1)/(3)(-4x^(-5))`
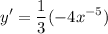
4. Simplify:
   `\displaystyle y' = (-4)/(3x^5)`

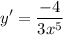
Topic: AP Calculus AB/BC (Calculus I/I + II)

Unit: Differentiation