Question

If this decay has half-life of 2 years, how many years would it take for 10.8 g Protactinium-231 to remain given an initial mass of 86.3 g?

Answer 1

Time = 6 years

Step-by-step explanation:

First, we will calculate the no. of half life periods required to reduce the mass of Protactinium to the given value:

`m' = (m)/(2^(n) ) \\\\2^n = (m)/(m')`

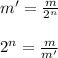
where,

n = no. of half-life periods = ?

m = initial mass = 86.3 g

m' = remaining mass = 10.8 g

Therefore,

`2^n = (86.3\ g)/(10.8\ g)\\\\2^n = 8\\2^n = 2^3`

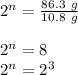
Since the bases are the same. Therefore equating powers:

n = 3

Now we calculate the time:

`Time = (n)(Half-Life)\\Time =(3)(2\ years)`

Time = 6 years