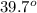Question

PLEASE HELP ME TO ANSWER THIS QUESTION.

A right pyramid PQRST has a rectangular base QRST. Given
that W is the midpoint of QS and RT, the lengths of QT = 8 cm,
TS = 6 cm and point P is vertically above point W, calculate
(a) PT, in cm, if PW = 12 cm
(b) the value of < PTR [angle PTR]

THANK YOU!!!​

Answer 1

(a) PT = 13 cm

(b) <PTR =
`39.7^(o)`

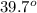
Explanation:

(a) Applying the Pythagoras theorem to QST, we have;

`QS^(2)` =
`ST^(2)` +
`QT^(2)`

=
`6^(2)` +
`8^(2)`

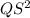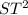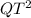
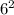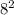
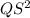`QS^(2)` = 36 + 64

100

QS =
`√(100)`

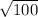
= 10

QS = 10 cm

Since QS = TR, then;

WT =
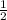`(1)/(2)` TR

=
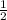`(1)/(2)` x 10

WT = 5 cm

Thus, applying Pathagoras theorem to PWT;

`PT^(2)` =
`PW^(2)` +
`WT^(2)`

=
`12^(2)` +
`5^(2)`

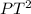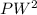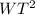
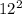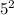
= 144 + 25

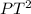`PT^(2)` = 169

PT =
`√(169)`

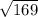
= 13

PT = 13 cm

(b) To determine <PTR, TR = 10 cm. Apply the required trigonometric function;

Cos θ =
`(adjacent)/(hypotenuse)`

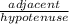
Cos θ =
`(10)/(13)`

= 0.7692

θ =
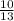
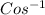`Cos^(-1)` 0.7692

= 39.7179

θ =
`39.7^(o)`

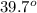
Therefore, <PTR =
`39.7^(o)`