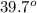Answer:
(a) PT = 13 cm
(b) <PTR =
Explanation:
(a) Applying the Pythagoras theorem to QST, we have;
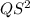 =
=
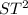 +
+
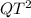
=
 +
+
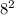
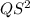 = 36 + 64
= 36 + 64
100
QS =
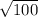
= 10
QS = 10 cm
Since QS = TR, then;
WT =
 TR
TR
=
 x 10
x 10
WT = 5 cm
Thus, applying Pathagoras theorem to PWT;
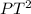 =
=
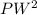 +
+

=
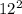 +
+
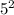
= 144 + 25
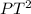 = 169
= 169
PT =
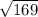
= 13
PT = 13 cm
(b) To determine <PTR, TR = 10 cm. Apply the required trigonometric function;
Cos θ =

Cos θ =
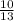
= 0.7692
θ =
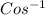 0.7692
0.7692
= 39.7179
θ =
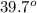
Therefore, <PTR =