Given:
The equation is:
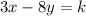
It cuts the x-axis and y- axis at the point A and B respectively.
The area of ∆AOB =12 sq.units.
To find:
The value of k.
Solution:
We have,
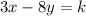
Substituting
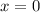 to find the y-intercept.
to find the y-intercept.



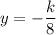
Substituting
 to find the x-intercept.
to find the x-intercept.
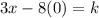

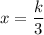
Area of a triangle is:
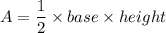
The height of the ∆AOB is
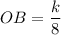 because distance cannot be negative and the base of the ∆AOB is
because distance cannot be negative and the base of the ∆AOB is
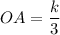 . So, the area of the ∆AOB is:
. So, the area of the ∆AOB is:
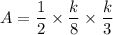
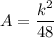
It is given that, the area of ∆AOB = 12 sq.units.
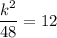
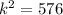
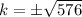
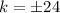
Therefore, the value of k is either 24 or -24.