Question

Anthony wants to find the value of k for which given points W(0,-2), I(2,0) and L(5,k) are collinear

A. K=-3

B. K=1/3

C. K=1/2

D. K=2

E. K=3

F. K=-1/3

Answer 1

Given:

The three points are W(0,-2), I(2,0) and L(5,k).

To find:

The value of k for which the given points are collinear.

Solution:

We know that, three points are collinear if the area of the triangle formed by these three points is 0.

`(1)/(2)|x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)|=0`

`x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)=0`

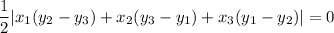
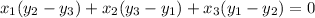
The three points are W(0,-2), I(2,0) and L(5,k). So,

`0(0-k)+2(k-(-2))+5(-2-0)=0`

`0+2(k+2)+5(-2)=0`

`2k+4-10=0`

`2k-6=0`

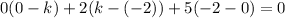
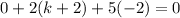
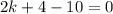
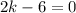
Adding 6 on both sides, we get

`2k=6`

`k=(6)/(2)`

`k=3`

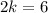
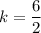
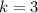
Therefore, the correct option is E.