Question

Can somebody explain how do I do this?

Answer 1

`\displaystyle \perp\:(1)/(2) \\ \parallel\:-2`

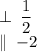
Explanation:

You must first transform this standard equation to a Slope-Intercept equation like so:

`\displaystyle y = mx + b \\ \\ -6x - 3y = -5 \hookrightarrow (-3y)/(-3) = (6x - 5)/(-3) \\ \\ \boxed{y = -2x + 1(2)/(3)}`

So, from this equation, we can tell that the y-intercept is at
`\displaystyle [0, 1(2)/(3)],`and the rate of change [slope] is −2, which is represented by
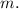`\displaystyle m.`Now, we want the information on the rate of change ONLY. Perpendicular graphs have OPPOCITE MULTIPLICATIVE INVERCE rate of changes, which means we take the oppocite of −2, then flip it, to get
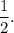`\displaystyle (1)/(2).`Parallel equations have SIMILAR rate of changes, so −2 remains as is.

I am joyous to assist you at any time.