Answer:
b)
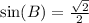
e)
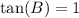
Explanation:
Given
The attached triangle
Required
The true statement about B
The given options show that we determine the correct trigonometry ratio of B.
So, we have:
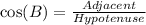
This gives:
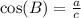
Where:
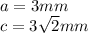
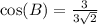
3 cancels out

Rationalize
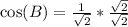
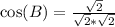
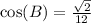
Also:
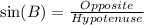
This gives:

Where:
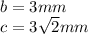

3 cancels out
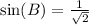
Rationalize
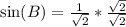

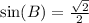
Lastly:

This gives:
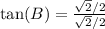
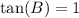
Hence, (b) and (e) are true