Answer:
(a) Same slope and different y intercept
Explanation:
Given
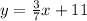
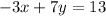
Required
Are the lines, parallel?
To do this, we first convert both equations to slope intercept;
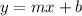
Where
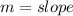
So, we have:
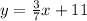
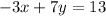
Solve for 7y
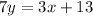
Solve for y
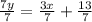
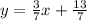
So, the two equations are now:
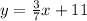
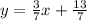
When two lines have the same slope but different y intercepts, then they are parallel.
Recall that:
In

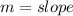
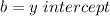
So:
In
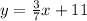 and
and
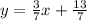
The slopes are:
 and
and

The y intercepts are:
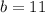 and
and
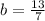
Since the values of m (the slope) are the same and the values of b (the y intercepts) are differenr, then they are parallel